El Premio Nobel de Economía que se arruinó en Bolsa

En 1997 la Academia sueca concedió el premio Nobel de Economía a Myron Scholes y Robert C. Merton por “un nuevo método para determinar el valor de los derivados”. Merton escribió que, antes de la teoría de la cartera, las finanzas eran “una colección de anécdotas, reglas de oro y manipulación de datos contables”. La teoría de la cartera –basada en los trabajos pioneros de otro premio nobel, Harry Markowitz– permitía “la evolución posterior de este popurrí conceptual a una teoría económica rigurosa”.

Merton y Scholes habían fundado tres años antes –junto con John Meriwether, antiguo vicepresidente de Salomon Brothers– un fondo de inversión libre de carácter especulativo, Long Term Capital Management o LTCM, con sede en Greenwich (Connecticut), que utilizaba estrategias de arbitraje combinadas con un elevado apalancamiento y que obtuvo elevados rendimientos en los primeros años. Todo el mundo les consideraba unos genios. Pero en 1998, a raíz de la crisis financiera rusa, sus modelos de riesgo se fueron al garete: el fondo perdió 4.600 millones de dólares en menos de cuatro meses, provocando la intervención de la Reserva Federal de los Estados Unidos, el rescate por otras entidades financieras y el cierre a comienzos de 2000.

No era el primer gran economista que se arruinaba. Ya a primeros de octubre de 1929 el entonces prestigioso economista Irving Fisher (para Milton Friedman “el mejor economista que EEUU jamás ha producido”) escribía en el New York Times que los precios de las acciones habían alcanzado “una meseta permanentemente alta”. Pero unos días después, el jueves 24 de octubre, el mercado cayó un 11%; un 13% el lunes siguiente y un 12% más el “martes negro”. Fisher insistió en que las caídas sólo podían ser temporales, pero a mediados de noviembre, cuando el Dow Jones había perdido casi la mitad de su valor anterior al accidente, la fortuna de Fisher se hundió junto con su reputación.

Uno hubiera pensado que Merton y Scholes habrían aprendido de Fisher. Y si no, al menos los economistas habrían aprendido de lo que les pasó a estos premios Nobel. Pero a la crisis financiera rusa le siguieron la crisis de las punto com y la Gran Recesión de 2008.

El problema, como ya advirtió en su día Nassim Taleb en su libro El Cisne Negro –que cumple ahora diez años–, se deriva de que la teoría de gestión de carteras se basaba en gran medida de hipótesis sobre variables financieras que en la realidad no se cumplen.

Así, dicha teoría suponía que todos los agentes disponían e interpretaban de la misma forma la misma información y que, por tanto, la posibilidad de obtener rendimientos de forma sostenida en el tiempo era prácticamente imposible. Asimismo, suponía que las variaciones de los rendimientos no tenían que ver unas con otras, es decir, que la caída de o subida de hoy no depende de la subida o caída de otras variables ni de la caída o subida en períodos anteriores. En términos estadísticos, se presuponía que los rendimientos seguían una distribución normal, en forma de campana de Gauss.

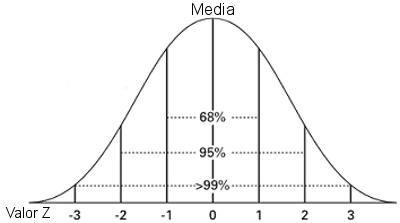
¿Qué implica que los rendimientos de una variable sigan una distribución normal? En el fondo, y de una forma muy simplificada, que la media y la varianza (o su raíz cuadrada, la desviación típica, una medida de la variabilidad respecto a la media) de una muestra nos permiten conocer de forma bastante precisa la realidad de la población. Así, por ejemplo, supongamos que se toma una muestra de la estatura de 1.000 personas y se obtiene una media de 170 cm y una desviación típica de 10 cm. Si asumimos que la estatura sigue una distribución normal, se tiene que cumplir que:

• El 68% de la población medirá 170 cm más/menos 10 cm (la media más/menos una desviación típica), es decir, entre 160 y 180 cm
• El 95% de la población medirá 170 cm más/menos 20 cm (la media más/menos dos desviaciones típicas), es decir, entre 150 y 190 cm
• El 99% de la población medirá 170 cm más/menos 30 cm (la media más/menos tres desviaciones típicas), es decir, entre 140 y 200 cm

Dicho de otra forma, nos permitiría calcular cuál es la probabilidad de que, tomada una persona al azar, tuviera una estatura determinada. Así, por ejemplo, la probabilidad de que una persona mida 220 cm, es decir, que sea un poquito más alta que Pau Gasol, y por tanto esté a 5 desviaciones típicas de la media sería de menos de 2 de cada 10 millones. Esto quiere decir que la probabilidad de encontrarnos con una estatura que se desvíe mucho de la media es difícil y, además que, si nos la encontramos, no alterará demasiado la media.

Aplicado a los mercados financieros, tomemos por ejemplo los rendimientos diarios del IBEX-35 entre enero de 2000 y abril de 2017, que presentan una desviación típica del 1,51%. Si siguieran una distribución normal, la probabilidad de que hubiera una caída superior al 6%, es decir, de 3,97 desviaciones típicas, sería de 1 vez cada 113 años. Sin embargo, en 17 años ha habido dos caídas superiores a esa cifra (una en 2008 y otra en 2016). Eso sería como construir una casa en una loma cerca de un río a una altura que se rebasa una vez cada 113 años, y 20 años después se ha inundado dos veces. ¿Qué cree que haría la compañía de seguros?

En realidad, la mayoría de los estudios que han contrastado la hipótesis de normalidad de los rendimientos de distintas variables financieras la han rechazado (ver aquí), mostrando que, en valores cercanos a la media, los rendimientos se comportan como una distribución normal, pero las colas, en especial la izquierda (las caídas) son mucho más gruesas de lo que cabría esperar de una distribución de ese tipo. En román paladino, eso quiere decir que la probabilidad de fuertes caídas inesperadas es muchísimo mayor de lo que podríamos pensar. Además, cualquier análisis de rentabilidades basado en extrapolaciones, o en regresiones por mínimos cuadrados, sería totalmente engañoso.

¿Cuál es la diferencia respecto al ejemplo que veíamos de la estatura? Que, en el caso de la estatura, alguna vez podremos encontrarnos personas que se desvíen mucho de la media, pero ni se desviarán en exceso (no hay nadie que mida 5 metros) ni los casos que encontremos alterarán sustancialmente la media. Por el contrario, en los mercados financieros, no solo habrá casos que se desvíen espectacularmente de la media, sino que hay posibilidades de que la media se altere sustancialmente: esto es, que durante tres años ganemos un 20% y en una semana lo perdamos todo.

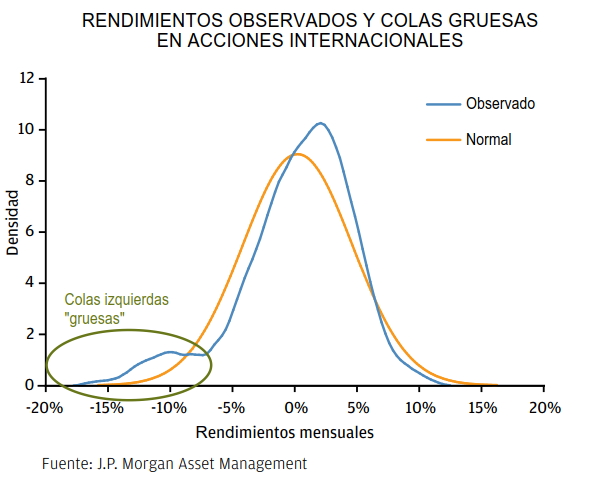
Uno pensaría que el rechazo de la hipótesis de normalidad llevaría a que todos los gestores de carteras utilizasen distribuciones alternativas a la normal que recogiesen adecuadamente la existencia de colas gruesas, la correlación y la autocorrelación, pero por desgracia es que en muchos casos no es así, y las rentabilidades medias y desviaciones típicas se siguen empleando para evaluar muchas inversiones.

Tenemos además que ser precavidos, ya que la hipótesis de normalidad puede ser más que dudosa en variables importantes como la distribución de la renta y la riqueza (en la que unos pocos multimillonarios pueden alterar por completo la media), o la climatología (ahora que se dice que el tifón Harvey solo ocurre una vez cada 500 años). El mundo, y nuestras vidas, están condicionadas por la posibilidad de un Cisne Negro, un suceso con los tres atributos siguientes: ser atípico (fuera del ámbito de las expectativas regulares, de modo que no hay nada en el pasado que puede apuntar de manera convincente a su posibilidad); producir un impacto extremo (no necesariamente negativo: la aparición de Internet o la penicilina fueron “cisnes negros” positivos); y que, a pesar de su rareza, la naturaleza humana (y el sesgo retrospectivo) nos haga inventar explicaciones del suceso, como si en realidad hubiéramos podido predecirlo.

Por desgracia, una de las características de la economía moderna es su complejidad. Por supuesto, existen herramientas estadísticas y analíticas que permiten en cierta medida modelizar dicha complejidad (así como distribuciones que reflejan mejor esas “colas gruesas”), pero debemos ser conscientes de que lo “normal” es mucho más infrecuente de lo que nos gustaría.

En su carta a los inversores de 2008, Warren Buffet escribió: “Creo que la fórmula de Black-Scholes, aunque es el estándar para establecer las opciones sobre pasivos en dólares, produce resultados extraños cuando se evalúa la volatilidad a largo plazo (…) La fórmula de Black-Scholes se ha aproximado al estatus de escritura sagrada en finanzas (…) Si la fórmula se aplica a períodos de tiempo prolongados, sin embargo, puede producir resultados absurdos. Para ser justos, en realidad Black y Scholes entendieron bien este punto. Pero sus devotos seguidores pueden estar ignorando las advertencias que ambos incluyeron al desvelar su fórmula”.

Algunos, todavía, siguen ignorándolas.