
Una ordenación personal de preferencias es transitiva, es decir, si frente a tres opciones A, B, y C; A se prefiere a B, y B se prefiere a C, se deduce que A será preferido a C. Sin embargo, ya en el año 1785, el ilustrado francés marqués de Condorcet llamó la atención sobre la no transitividad de preferencias en los sistemas electorales, de manera que el orden en el que se plantean las alternativas afecta al resultado final. ¿Constituye la moción de censura presentada por Pedro Sánchez un ejemplo de intransitividad de preferencias, en este caso, comparada con las opciones de la moción “instrumental” y la dimisión de Mariano Rajoy? No está claro.
Veamos un ejemplo sencillo. Si suponemos un cuerpo electoral de 100 personas que deben votar entre tres alternativas A, B y C, siendo sus preferencias las siguientes:

Los resultados entre las alternativas A, B y C variarían en función de cómo planteáramos la elección. En una votación conjunta de las tres alternativas ganaría: A (41votos), seguida de B (30 votos), y de C (29 votos), es decir genera una ordenación A> B > C. Sin embargo, si la comparación se hace por pares, obtendríamos:

Este resultado implica una ordenación C > B > A, justamente la contraria a la que produce la votación conjunta.
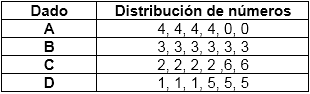
Los trabajos de Condorcet en los que se destacaban estas incoherencias han tenido influencia en el diseño de sistemas electorales. Un caso muy ilustrativo de intransitividad son los dados de Efron (desarrollados por el estadístico Bradley Efron), un conjunto de cuatro dados cuyas caras tienen los siguientes números:
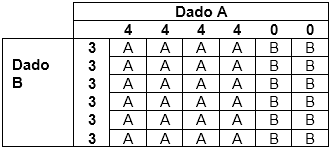
Supongamos un juego entre dos jugadores en el que cada uno de ellos elige uno de los cuatro dados. Sean estos dados A y B. Para comparar los resultados que pueden obtenerse jugando con los dados A y B, en el cuadro adjunto se han colocado en la cabecera de las columnas los posibles resultados con el dado A y en la cabecera de las filas con el dado B. Obtenemos así una cuadricula de 36 posiciones con las diferentes combinaciones que puedan darse al lanzar ambos dados. En cada cuadrícula aparece indicado el dado ganador correspondiente al resultado definido por su fila y columna. A ganaría en 24 combinaciones y B en 12, es decir la probabilidad de ganar con A sería de 2/3.
Ahora bien, si se hace el mismo ejercicio comparando el resto de pares de dados obtendríamos los siguientes resultados:

Si empezáramos a comparar los dados en el mismo orden de este cuadro, A con B, B con C y C con D, los resultados nos llevarían a una ordenación de preferencias en función de la probabilidad de ganar: A> B > C > D. Sin embargo, la relación no es transitiva porque puede verificarse que D es preferible a A, también por 24 a 12. Es un resultado contrario a nuestra intuición y tiene curiosas implicaciones. Si dos jugadores compiten cada uno con un diferente dado de Efron para obtener la mayor puntuación, ofreciendo al contrario la “cortesía” de elegir dado en primer lugar, el segundo jugador estará en ventaja porque siempre tendrá la opción de elegir un dado más favorable sea cual sea la elección del primero.
En definitiva, el orden en el que planteemos las alternativas afecta al resultado final. En este sentido, la presentación por el PSOE de la reciente moción de censura puede asemejarse a una ordenación no transitiva. Solamente el PSOE y Podemos estaban capacitados por su número de diputados a presentar una moción de censura. El PSOE se anticipó presentando una moción que resultó ganadora.
Sin embargo, dado el equilibrio de votos existente, una moción “instrumental” presentada por Podemos, proponiendo un candidato independiente y la convocatoria inmediata de elecciones, hubiera salida con mayor holgura: Ciudadanos la habría apoyado y difícilmente el PSOE podía bloquearla. Se podría así establecer una relación de preferencia en cuanto a la capacidad para ganar la moción de censura del tipo: moción Podemos > moción PSOE > opción PP.
¿Esta ordenación es intransitiva? En otros términos, ¿tenía el PP la posibilidad de contrarrestar la moción de censura con la dimisión de Mariano Rajoy?
La aritmética parlamentaria no avalaba esta posibilidad porque la moción de censura salió adelante por 180 contra 169 votos (PP, Ciudadanos, UPN y Foro Asturias) con una abstención de Coalición Canaria. La dimisión de Mariano Rajoy y presentación de un candidato del PP consensuado con el PNV (y con Ciudadanos) podía contar con los 5 votos del PNV y el de Coalición Canaria, lo que supondría 175 votos, insuficientes para una investidura –hace falta mayoría absoluta (al menos 176 votos), en primera vuelta, y más votos a favor que en contra, en segunda vuelta–. Por otra parte, no hay razones para pensar que el bloque de apoyo a la moción de censura se rompiera en el caso de una investidura de Pedro Sánchez, entre otros motivos porque ello significaría convocatoria de elecciones, opción generalmente no favorecida por los integrantes de dicho bloque.






